Giải Toán 7 Bài 3: Hai đường thẳng song song hướng dẫn giải bài tập trong SGK Toán 7 Chân trời sáng tạo tập 1 trang 76, 77, 78, 79, 80, 81, giúp các em nắm vững kiến thức được học trong bài, luyện giải Toán 7 hiệu quả. Sau đây mời các bạn tham khảo chi tiết.
Khởi động trang 76 SGK Toán 7 tập 1 CTST
Hai đường thẳng a và b không có điểm nào chung thì được gọi là hai đường thẳng song song và được kí hiệu là a // b hoặc b // a.
- Có dấu hiệu gì về số đo của các góc đỉnh A và các góc đỉnh B trong hình bên để nhận biết hai đường thẳng a và b song song hay không?
Đáp án:
Sau khi học bài học ta rút được kết luận:
Để nhận biết hai đường thẳng a và b song song với nhau hay không ta kiểm tra các cặp góc so le trong bằng nhau hoặc các cặp góc đồng vị bằng nhau.
Khám phá 1 trang 76 SGK Toán 7 tập 1 CTST
Quan sát Hình 3 và dự đoán các đường thẳng nào song song với nhau.
Đáp án:
Dự đoán các đường thẳng song song với nhau là:
a // b
m // n
Thực hành 1 trang 77 Toán 7 Tập 1:
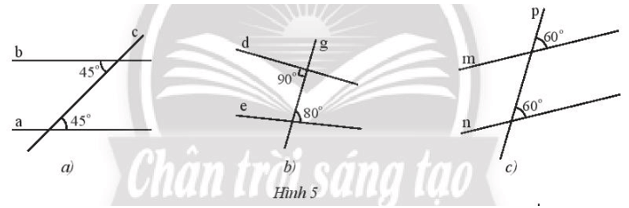
Tìm các cặp đường thẳng song song trong Hình 5 và giải thích.
Thực hành 2 trang 77 SGK Toán 7 tập 1 CTST:
Cho hai đường thẳng phân biệt a và b cùng vuông góc với đường thẳng c tại A và B (Hình 6). Hãy chứng tỏ a // b.
Đáp án:
Kí hiệu hình vẽ như sau:
Ta có: a ⊥ c =>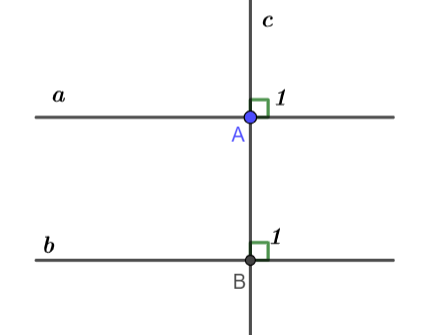 
(widehat {{A_1}} = {90^0})
b ⊥ c => (widehat {{B_1}} = {90^0})
=> (widehat {{A_1}} = widehat {{B_1}} = {90^0})
Mà hai góc (widehat {{A_1}};widehat {{B_1}}) nằm ở vị trí so le trong
=> a // b
Khám phá 2 trang 78 SGK Toán 7 tập 1 CTST
Cho điểm A nằm ngoài đường thẳng a, quan sát cách vẽ đường thẳng b đi qua A và song song với a ở Hình 8.
Em hãy dự đoán xem có tất cả bao nhiêu đường thẳng b đi qua A và song song với đường thẳng a.
Đáp án:
Vẽ hình theo các bước như trên Hình 8.
Dự đoán: có một đường thẳng b đi qua A và song song với đường thẳng a.
Thực hành 3 trang 79 Toán 7 Tập 1:
a) Cho tam giác ABC. Hãy nêu cách vẽ đường thẳng a đi qua đỉnh A và song song với BC, cách vẽ đường thẳng b đi qua đỉnh B và song song với AC.
b) Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?
Đáp án:
Đo góc ABC. Vẽ đường thẳng a đi qua A sao cho góc tạo bởi a và đường thẳng AB bằng góc ABC.
Ta được đường thẳng a đi qua A và song song với BC
Đo góc ACB. Vẽ đường thẳng b đi qua B sao cho góc tạo bởi b và đường thẳng BC bằng góc ACB.
Ta được đường thẳng b đi qua B và song song với AC
b) Có thể vẽ được chỉ 1 đường thẳng a, 1 đường thẳng b thoả mãn yêu cầu. Vì qua 1 điểm nằm ngoài một đường thẳng, chỉ có 1 đường thẳng song song với nó
Khám phá 3 trang 79 Toán 7 Tập 1:
Em hãy:
- Vẽ hai đường thẳng a và b song song với nhau.
- Vẽ đường thẳng c cắt đường thẳng a và b lần lượt tại A và B.
a) Chọn và đo một cặp góc so le trong, so sánh cặp góc này.
b) Chọn và đo một cặp góc đồng vị, so sánh cặp góc này.
Đáp án:
a) Một cặp góc so le trong là góc A3 và góc B1 . Hai góc này cùng có số đo là 600 nên chúng bằng nhau .
b) Một cặp góc đồng vị là góc A1 và góc B1 . Hai góc này cùng có số đo là 600 nên chúng bằng nhau .
Thực hành 4 trang 79 SGK Toán 7 tập 1 CTST
Cho biết m // n và a // b. Tính số đo x, y, z, t của các góc trong Hình 12.
Đáp án:Kí hiệu hình vẽ:
Xét hình 12a
Ta có: m // n
=> (x = widehat {ACD} = {45^0}) (Hai góc đồng vị)
Ta cũng có: (y = widehat {ABD} = {80^0}) (Hai góc so le trong)
Vậy x = 450; y = 800
Xét hình 12b
Ta có: a // b => (widehat {{M_1}} = widehat {MNF} = {60^0})
Mặt khác: (widehat {{M_1}} + widehat {NME} = {180^0}) (Hai góc kề bù)
=> (widehat {MNF} = {180^0} - widehat {{M_1}} = {180^0} - {60^0} = {120^0})
=> z = 600
Ta có: a // b => (t = widehat {EFN} = {90^0}) (Hai góc so le trong)
Vận dụng 1 trang 80 SGK Toán 7 tập 1 CTST:
Tìm các cặp góc bằng nhau của hai tam giác ABC và DEC trong Hình 13, biết a // b.
Đáp án:Ta có: a // b
=> (widehat {CBA} = widehat {CED}) ; (widehat {BAC} = widehat {EDC}) (hai góc so le trong)
Ta lại có:
(widehat {BCA} = widehat {CDE})(Hai góc đối đỉnh)
Vậy các cặp góc bằng nhau của tam giác ABC và DEC là (widehat {CBA} = widehat {CED}); (widehat {BAC} = widehat {EDC}); (widehat {BCA} = widehat {CDE})
Vận dụng 2 trang 80 SGK Toán 7 tập 1 CTST
Cho hai đường thẳng a, b song song với nhau, đường thẳng c vuông góc với a tại A và cắt b tại B. Hãy giải thích tại sao đường thẳng c cũng vuông góc với b.
